¿Qué es la estadística descriptiva?
La estadística descriptiva es la rama de la estadística que recolecta, analiza y caracteriza un conjunto de datos (peso de la población, beneficios diarios de una empresa, temperatura mensual,…) con el objetivo de describir las características y comportamientos de este conjunto mediante medidas de resumen, tablas o gráficos.
Variables estadísticas
Una variable estadística es el conjunto de valores que puede tomar cierta característica de la población sobre la que se realiza el estudio estadístico y sobre la que es posible su medición. Estas variables pueden ser: la edad, el peso, las notas de un examen, los ingresos mensuales, las horas de sueño de un paciente en una semana, el precio medio del alquiler en las viviendas de un barrio de una ciudad, etc.
Las variables estadísticas se pueden clasificar por diferentes criterios. Según su medición existen dos tipos de variables:
- Cualitativa (o categórica): son las variables que pueden tomar como valores cualidades o categorías.
Ejemplos:
- Sexo (hombre, mujer)
- Salud (buena, regular, mala)
- Cuantitativas (o numérica): variables que toman valores numéricos.
Ejemplos:
- Número de casas (1, 2,…). Discreta.
- Edad (12,5; 24,3; 35;…). Continua.
Medidas de posición central
Las medidas de tendencia central (o de centralización) son medidas que tienden a localizar en qué punto se encuentra la parte central de un conjunto ordenado de datos de una variable cuantitativa.
Media
Definimos media (también llamada promedio o media aritmética) de un conjunto de datos (X1,X2,…,XN) al valor característico de una serie de datos resultado de la suma de todas las observaciones dividido por el número total de datos.
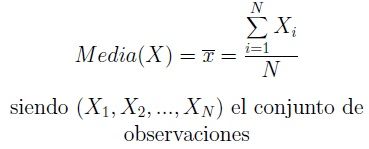
Es decir:


Visto desde un punto de vista más conceptual, la media aritmética es el centro de los datos en el sentido numérico, ya que intenta equilibrarlos por exceso y por defecto. Es decir, si sumamos todas las diferencias de los datos a la media da cero.

Mediana
La mediana (Me(X)) es el elemento de un conjunto de datos ordenados (X1,X2,…,XN) que deja a izquierda y derecha la mitad de valores.

Si el conjunto de datos no está ordenado, la mediana es el valor del conjunto tal que el 50% de los elementos son menores o iguales y el otro 50% mayores o iguales.
Moda
La moda (Mo(X)) es el valor más repetido del conjunto de datos, es decir, el valor cuya frecuencia relativa es mayor. En un conjunto puede haber más de una moda.

Media geométrica
La media geométrica (MG) de un conjunto de números estrictamente positivos (X1, X2,…,XN) es la raíz N-ésima del producto de los N elementos.
Todos los elementos del conjunto tienen que ser mayores que cero. Si algún elemento fuese cero (Xi=0), entonces la MG sería 0 aunque todos los demás valores estuviesen alejados del cero.

Media armónica
La media armónica (H) de un conjunto de elementos no nulos (X1, X2,…,XN) es el recíproco de la suma de los recíprocos (donde 1/Xi es el recíproco de Xi)) multiplicado por el número de elementos del conjunto (N).

Media cuadrática
La media cuadrática o RMS (Root Mean Square) de un conjunto de valores (X1, X2,…,XN) es una medida de posición central. Esta se define como la raíz cuadrada del promedio de los elementos al cuadrado.


Media ponderada
La media ponderada (MP) es una medida de centralización. Consiste en otorgar a cada observación del conjunto de datos (X1,X2,…,XN) unos pesos (p1,p2,…,pN) según la importancia de cada elemento.

Cuanto más grande sea el peso de un elemento, más importante se considera que es éste.
Relación entre medias
Existe una relación de orden entre cuatro tipos de media. En esta relación se excluye la media ponderada porque depende de los pesos. Sean:
- H la media armónica
- MG la media geométrica
- x la media aritmética
- RMS la media cuadrática
Entonces:
En esta relación, solamente se cumple la igualdad cuando todos los datos sean iguales, es decir si: x1 = x2 = x3 = … = xN.
Medidas de posición no central
Las medidas de posición no central (o medidas de tendencia no central) permiten conocer puntos característicos de una serie de valores, que no necesariamente tienen que ser centrales. La intención de estas medidas es dividir el conjunto de observaciones en grupos con el mismo número de valores.
Cuartiles
Los cuartiles son los tres valores que dividen una serie de datos ordenada en cuatro porciones iguales. El primer cuartil (Q1) deja a la izquierda el 25% de los datos. El segundo (Q2) deja a izquierda y derecha el 50% y coincide con la mediana. El tercero (Q3) deja a la derecha el 25% de valores. Los tres cuartiles son:

Percentiles
El percentil es una medida de posición no central. Los percentiles Pi son los 99 puntos que dividen una serie de datos ordenada en 100 partes iguales, es decir, que contienen el mismo número de elementos cada una. El percentil 50 es la mediana.
Sea (X1, X2,…,XN) una muestra de N elementos. El percentil Pi es:

Donde Pi es la posición del percentil buscado en la serie ordenada de datos.
Los percentiles están pensados para conjuntos de elementos de más de cien elementos.
Medidas de dispersión
Las medidas de dispersión o medidas de variabilidad muestran la variabilidad de un conjunto de datos, indicando la mayor o menor concentración de datos respecto a las medias de centralización.
Rango
El rango (R) o recorrido estadístico es la diferencia entre el valor máximo y el mínimo de un conjunto de elementos.
Rango intercuartílico
El rango intercuartílico (IQR) (o rango intercuartil) es una estimación estadística de la dispersión de una distribución de datos. Consiste en la diferencia entre el tercer y el primer cuartil. Mediante esta medida se eliminan los valores extremadamente alejados. El rango intercuartílico es altamente recomendable cuando la medida de tendencia central utilizada es la mediana (ya que este estadístico es insensible a posibles irregularidades en los extremos).

En una distribución, encontramos la mitad de los datos, el 50 %, ubicados dentro del rango intercuartílico.
Conforme aumente el IQR, indicará que la dispersión será mayor.
Varianza
La varianza (S2) mide la dispersión de los datos de una muestra respecto a la media, calculando la media de los cuadrados de las distancias de todos los datos.

Al elevar las diferencias al cuadrado se garantiza que las diferencias absolutas respecto a la media no se anulan entre si. Además, resaltan los valores alejados.


GHCF YGUF G GJ GJKHKHL
ResponderEliminar